|
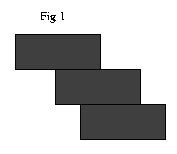
Sometimes asking silly questions leads us to discover not so silly, and very unexpected, answers. Here the question is this, suppose we are given a pile of bricks, just bricks mind you, no cement nor mortar, and we are asked to take the bricks and stack them one on top of the other, so that they don't fall over, but reach from here to China. Take a look at fig. 1 to see what I mean. I'm sure your immediate reaction is, "that's crazy," I know mine was. Probably your second reaction is, "Well, if Henry is writing about this, I'd better be careful." Sometimes it is wise not to rely on your first impulse. |
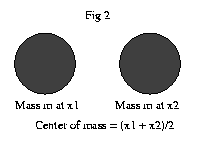
|
All we need to attack this problem this problem is to understand the concept of "center of mass." Intuitively, if you have some irregularly shaped object, the center of mass is the point in the object where you could balance it on the head of a pin. For example, the center of mass of a human body is somewhere around the solar plexus. If you remember as a kid balancing yourself on top a fencepost, the spot that you stuck your belly on is pretty close to your center of mass. Now take a look at fig 2. What is the center of mass of this system? Well, that's simple, it is just halfway between the two balls in the picture. If the balls were connected by a rod, we could balance the two of them on the tip of a pin at this point. |
| Now take a look at fig 3 and suppose that the two masses are not the same. The expression for the center of mass is a little more complicated now, but if you look at it, you can see that it is just what we call the "weighted average." This is what you would expect, as the center of mass should shift towards the heavier object. What does all this have to do with building a bridge to China? Well, in order to keep the bricks from toppling over, we need to make sure that the center of mass of the bricks that are on top of the bottom brick don't move past the edge of that bottom brick. |
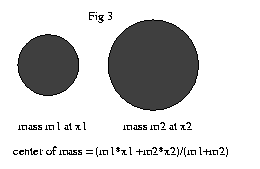
|
Let's see how that works out for the first few bricks. It may seem a little strange, but we are building this bridge from the top down, at least during the planning phase. Once we have a plan, we can build it from the bottom up, as you would expect. Anyway, the topmost brick can protrude halfway over the brick beneath it, since the center of mass of the top brick is in the exact middle of the brick. Let's assume, to keep things simple that each brick is 1 foot long. Also lets call the point where the topmost brick starts 0. Thus the location of the COM(Center Of Mass) of the top brick is 1/2. Now the edge of next brick that we put underneath the first two should be at the center of mass of the two bricks above it. Where is this? Well, the COM of the first brick is at 1/2, and the center of mass of the second brick is at 1/2 ( left edge of the brick + right edge of the brick) = 1/2(1/2 + (1/2 + 1)) = 1 so the COM of the two brick system is 1/2( COM of brick1 + COM of brick 2) = 1/2(1/2 + 1) = 3/4. Let's see if we can figure out the general case. Suppose we have already stacked up n bricks, where n is some number. We want to put brick number n+1 at the COM of the n brick system, and figure out what the new COM is for the new n+1 brick system. Lets call the position of the COM of the n brick system C(n). To find C(n+1) we need to take the weighted average of the n brick system and the new 1 brick system whose left edge is at C(n) (the old COM). Thus we have:
C(n+1) = 1/(n+1) * (n*C(n) + 1/2(C(n) + (C(n)+1))).
^^^^^^ right edge of new
brick
^^^ left edge of new brick
^^^^^^^^^^^^^^^^^^^ COM of new brick
^^^^^ weight of COM of n bricks * position
^^^^^^ Divide by total weight of the (n+1) brick system
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ weighted average
We can simplify the expression on the right hand side a lot, first by noticing that 1/2(C(n) + (C(n)+1)) = C(n) + 1/2. Then we have that n*C(n) + C(n) + 1/2 = (n+1)*C(n) + 1/2. Thus finally we get:
C(n+1) = 1/(n+1) * ((n+1)*C(n) + 1/2) = C(n) + 1/(2*(n+1))
What this means is that the COM of the n+1 brick system is located 1/(2*(n+1)) over from the COM of the n brick system. Another way of saying this is that after putting down n bricks, we have moved the center of mass from 0 to 1/2 + 1/4 + 1/6 + 1/8 ... + 1/(2n). Another way of writing this is to take out the common factor of 1/2 and then the rest becomes 1/2 * (1 + 1/2 + 1/3 + 1/4 ... + 1/n).
Now the question of whether we can reach China boils down to adding up a lot (a lot) of numbers, namely the (infinite) series 1 + 1/2 + 1/3 + ... (It's always those ...'s that kill you) Now the idea of adding up an infinite number of numbers has been around since the ancient Greeks. You might have heard of Zeno's paradox, where he "proves" that if you shoot an arrow at a tree the arrow never reaches the tree. How does he "prove" this? Well, Zeno said: consider the time it takes for the arrow to get halfway to the tree. Now cut that time in half and the arrow again is halfway between where it was and the tree. Cut that time in half and the arrow is again only halfway between where it was and the tree. Continuing in this way we can see that the arrow never reaches the tree. What Zeno was trying to do is add up the series 1/2 + 1/4 + 1/8 + 1/16 + ... 1/(2^n). He knew that no matter how many terms you add to this series, the sum never reaches the number 1. It gets as close as you like, but it never gets there. Mathematicians say that the series converges to 1, which is a fancy way of saying that it gets as close as you like, but it never gets there. What about our series, namely 1 + 1/2 + 1/3 + ..., does it converge to something, and if so what? I fired up my trusty computer and added the first 100 terms of the series. It came up with 5.17... After 1000 terms the answer was 7.48... So maybe it converges to 10, eh?
Before we get to the answer, I hope you will all agree that the series 1+1+1...+1 doesn't converge to any number, it just continues to get bigger and bigger. Similarly the series 1/2 + 1/2 + 1/2 ... keeps growing, it just takes twice as long. Now lets look at the first two numbers in our series, namely 1 and 1/2. Each of them is bigger than 1/2, so our series is bigger than 1/2 + 1/2. Now lets look at the next two terms, which are 1/3 and 1/4, both of which are greater than or equal to 1/4, and there are 2 of them so their sum is greater than 2 * 1/4 = 1/2. Now lets look at the next 4 terms, which are 1/5 + 1/6 + 1/7 + 1/8. Each of them is greater than or equal to 1/8, and there are 4 of them so their sum is bigger than 4 * 1/8 = 1/2. We can continue in this way always taking twice as many terms and noticing that their sum will alway be bigger than 1/2. Thus the sum of our series is bigger than the sum of the 1/2 + 1/2 + 1/2 ... series, which we've already admitted keeps on growing. What this means is that if we place our bricks according to this plan, we can span any distance we like, even going all the way to China. As Gomer Pyle used to say, surprise, surprise surprise.
One final note. We might ask how many bricks it would take to get to China. Well, if each brick is 1 foot long, I can tell you that using this scheme it would take about half a million bricks to go 10 feet. Maybe it's not the most practical scheme, but hey, I was a math major not an engineering major, and it is possible, IN THEORY!
Nadine and Henry wish you a theoretically perfect but practically wonderful New Year. Adios.
Dogs are not our whole life, but they make our lives whole.
Roger Caras
Sitemap
Go up to How do Things Work Go up to Home Page of Nadine Loves Henry
Go back to On Hurricanes and Bathtub Drains Continue with What's the difference between a Slug an a Newton